Pythagorean Theorem

In my last trip from Queretaro to Juarez (yeah, a lot happenned during that trip, jeje), we left my mom in Chihuahua (she had some family stuff to take care off) so it was only my dad and me in that last four-hour drive to Juarez. Both of us are real math hobbyist, and for some reason we ended up talking about the pythagorean theorem and the fact that neither of us, even though we use it for everything now, haven't seen it's proof in any text book we've read. It's such a used theorem, that it's difficult to think a proof for it. I remembered one, using the areas of the squares formed by the each of the sides of the right triangle, but that it's just a case-by-case proof, I'm more into generalized theorems.

Anyway, I had a small notebook with me so, with three hours of boredom ahead, I decided to prove it. An hour and a half later (which frankly felt more as half an hour), this is what I came up with:

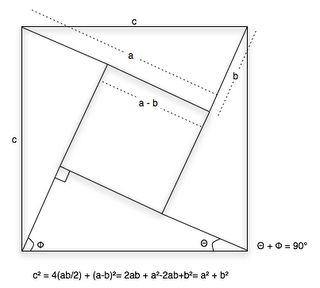
The equation on the bottom starts with an equality of areas: the area of the big square is the square of c, which also is equal to the sum of the area of the four right triangles and the area of the small square; it's just simple algebra from there on.

After I got home, I did a little research and imagine my surprise when I read that this theorem has around 370 proofs, all using from trigonometry, calculus, to finite math. Apparently my proof was actually done around two and half millenium ago, documented in the chinese text Chou Pei Suan Ching done between the year 500 to 200 BC, which right now is the first official documentation of a proof for such theorems; there have been others before, but none of them were documented for that purpose (it was more of a collateral thing in those). Actually, this proof is so famous in China that the Pythagorean Theorem is better known as "Gougu Theorem", based on the numerical proof in the Chou Pei Suan Ching, presented in The Arithmetical Classic of the Gnomon and the Circular Paths of Heaven.

In all fairness, the mayority of those proofs used trigonometry and calculus which, in themselves, use the pythagorean theorem for their own internal proofs (which sounds incongruent). The Chou Pei Suan Ching proof (mine) uses algebra and analytical geometry which doesn't rely on Pythagoras to be proven. So... yeah, I rock, jeje.

[This post was heavily based on the wikipedia article of The Pythagorean Theorem.]

EDIT: After further research I found that the Chou Pei Suan Ching proof was just for the case of the (3,4,5) triangle; it wasn't a general proof like mine. The first person to have actually proven it like I did was the Indian mathematician-astronomer Bhaskara Achārya; you can see evidence of this if you look him up, or in the first Addendum of this page.